密码技术入门
《图解密码技术》读书笔记,简要概括对称加密、非对称加密、散列函数、MAC、数字签名和伪随机数生成器的基本原理。
我们直接跳过凯撒密码、简单替换密码等只具有历史意义的知识......
对称加密
DES
DES(Data Encryption Standard)是一种将 64bit 明文加密为等长密文的对称加密算法,其密钥长度为 64bit(每隔 7 位插入一个用于错误检查的位)。
对于 64bit 的明文输入,DES 算法按照下图步骤进行若干轮的加密:
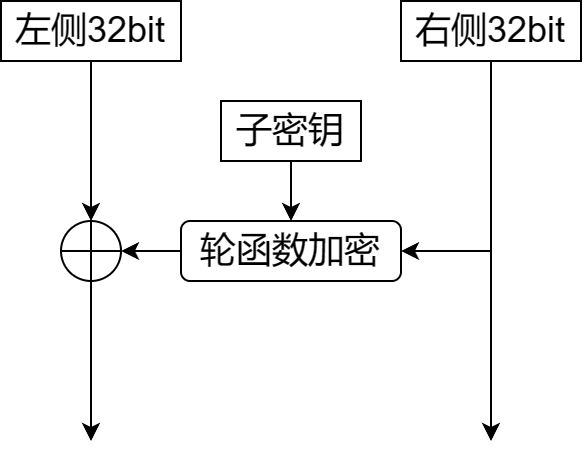
- 明文被分为左右各 32 位。
- 右侧明文和子密钥一起经过轮函数,得到 32 位的输出。
- 轮函数输出同左侧明文异或。
可见,一轮加密只能加密一半数据,因此需要多轮加密,每次左右两侧的输入分别为上一轮的右侧和左侧的输出。子密钥只是一个局部密钥,在每一轮中都有所不同。如果要解密,只需要逆序使用多轮加密的子密钥即可,(考虑一下 XOR 的特性: A XOR B XOR B = A )。
3DES 算法是对 DES 算法的改进,大意是使用三种密钥顺序运行 DES 算法三次,过程为 加密-解密-加密 ,中间加入解密步骤是为了和 DES 算法兼容。
AES (Rijndael)
AES(Advanced Encryption Standard)的输入分组为 128bit,即 16 字节,这 16 字节可以用一个 4x4 的矩阵表示,其一轮加密流程如下:
- 使用一张有 256 个值的替换表对矩阵中的每个字节进行替换(类似简单替换密码)。
- 将每行循环左移不同的位数(类似加强版的凯撒密码)。
- 对每一列进行混淆。
- 将处理后的矩阵与轮密钥进行异或。
与 DES 相比,AES 每次都能对全部明文进行处理,因此加密所需轮数更少。
分组密码的迭代模式
像 AES 和 DES 这样的加密算法,每次都只能对固定长度的明文输入进行加密,如果要加密任意长度的明文,则需要迭代运行加密算法。
ECB
一种简单的思路是将明文分成若干个固定长度的分组,然后对每个分组进行加密,这种模式称为 ECB(Electronic Codebook)。由于每个分组互不影响,这种模式还可以并行加密,效率较高。然而,恶意攻击者只需要了解加密数据的格式,就可以通过交换分组顺序的方式对数据进行篡改,甚至不需要破译加密算法的密钥。
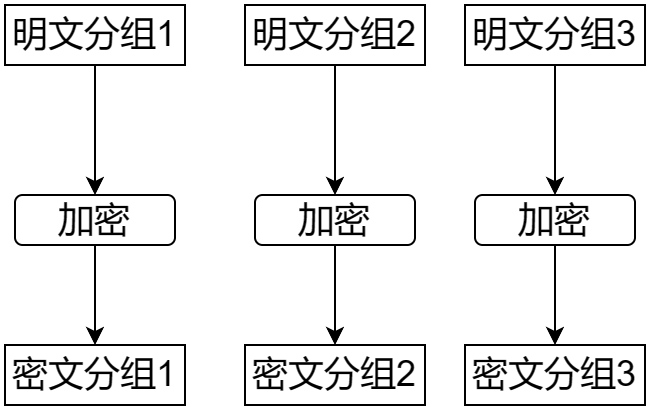
例如,如果一个计算机的密钥配置文件使用 ECB 模式加密:
密文分组1:用户名
密文分组2:密码攻击者只需要了解这个文件是以(用户名,密码)格式存储的,就可以直接用分组 1 的内容覆盖分组 2,从而修改用户的密码,达到侵入系统的目的。除此以外,如果明文分组的出现次数存在某种规律,则攻击者或许可以通过这种统计规律来破译密钥(这和简单替换密码类似)。
CBC
ECB 模式的弱点在于每个分组独立加密,而 CBC(Cipher Block Chaining)模式则在每个分组加密前都会与上一个分组的密文进行异或,这样就使得每个分组都依赖于前一个分组,从而使得攻击者无法直接修改分组内容,第一个分组则和一个随机的初始化向量 IV 进行异或(我们可以把 CBC 模式看作一个带有虚拟头节点的分组链表)。由于每个分组都和钱一个分组的密文相关,相同分组的密文也就不一定相同,因此 CBC 模式可以有效避免 ECB 模式的统计攻击。
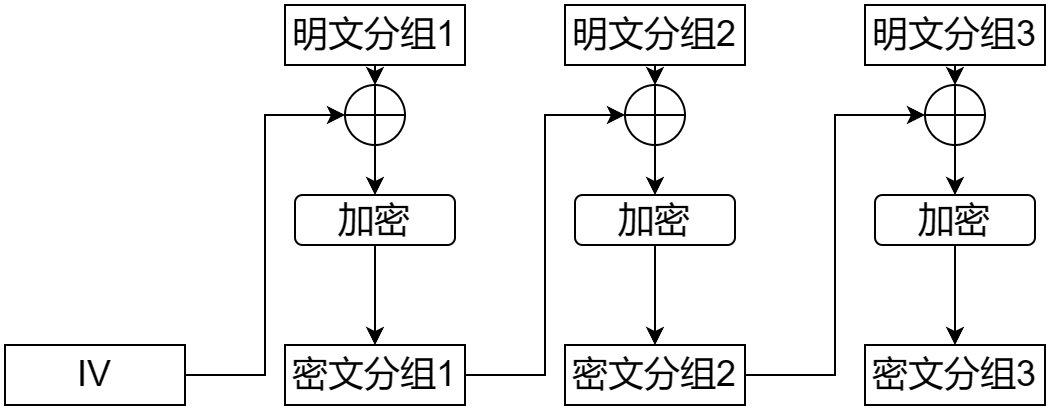
CBC 的缺陷在于,如果某个分组的密文被损坏,则会影响两个分组的解密。如果损坏导致一些密文的比特丢失,则将影响后续所有分组的解密。
CFB
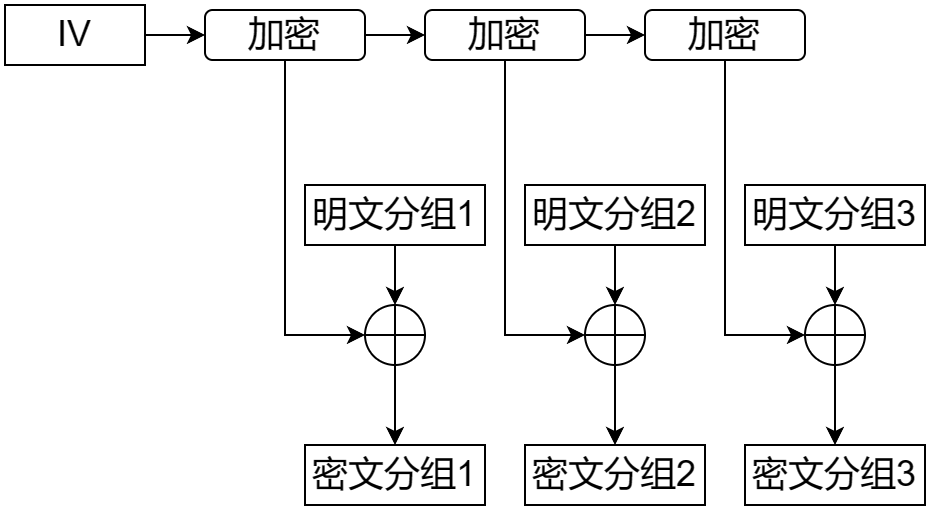
CFB(Cipher Feedback)模式将前一个分组作为加密算法的输入,然后将加密算法的输出与当前分组的明文进行异或,从而得到当前分组的密文。第一个分组同样需要一个随机的初始化向量 IV。
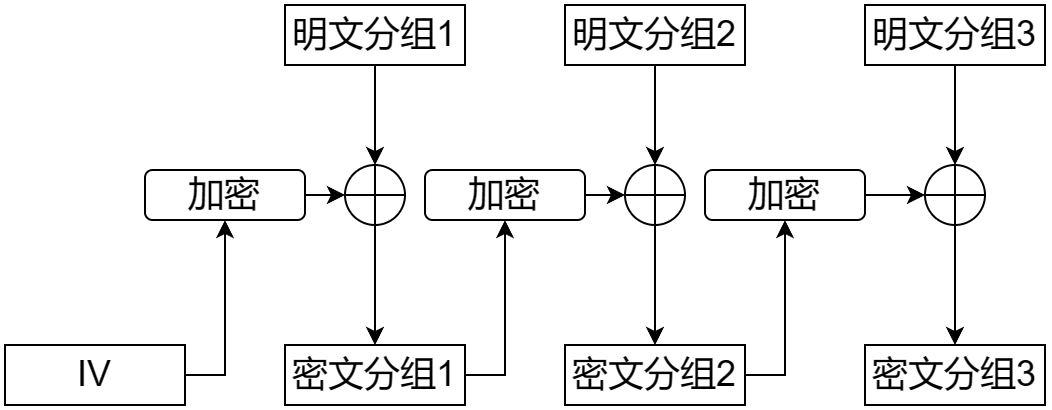
OFB
OFB(Output Feedback)模式和 CFB 模式类似,只是将加密算法的输出作为下一个分组的输入,而不是前一个分组的密文。
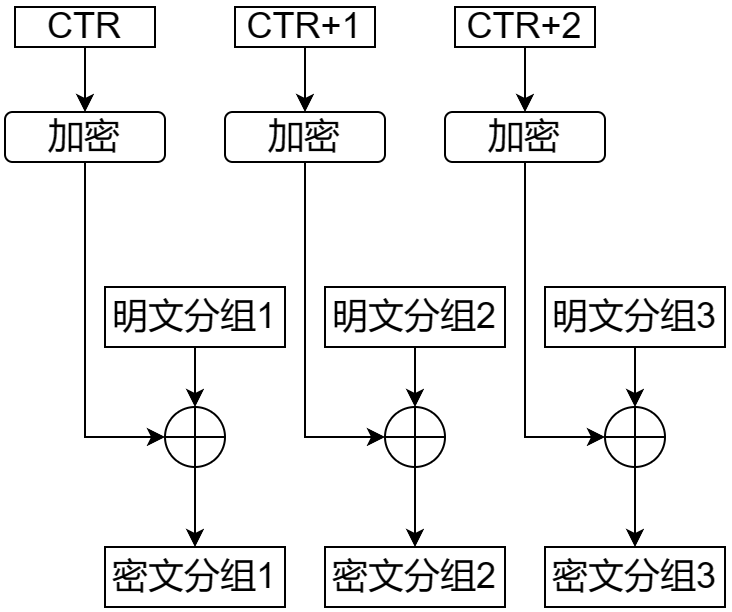
CTR
CTR(Counter)模式将一个计数器作为加密算法的输入,参与加密。计数器的值分为 nonce 和分组序号两个部分,前者在每次加密时都随机生成,后者严格递增。这种模式支持以任意顺序对分组进行加密解密,只需要提前根据分组序号和 nonce 计算出计数器值即可,这也就意味着可以并行加密解密。
非对称加密
使用对称加密算法,就一定要解决密钥配送问题,这是因为密钥同时被用来加解密,一旦泄露则将导致加密失效。而非对称加密算法用公钥进行加密,私钥进行解密,通信双方只需要交换公钥,用彼此的公钥加密数据即可,窃听者即使能够获取公钥,也无法解密数据。问题在于,在缺乏身份认证机制的情况下,第三方可能插入到双边通信的过程中,对任意一方冒充另一方,从而达到窃取信息的目的。
RSA
RSA(Rivest–Shamir–Adleman)算法可用于非对称加密和数字签名,其加解密过程如下:
密文 = 明文 ^ e mod n
明文 = 密文 ^ d mod ne 和 n 的组合即公钥,d 和 n 的组合即私钥。
在生成密钥对时,首先准备两个很大的质数 p 和 q,然后计算 n = p * q,再计算 $n = p * q
对恶意攻击者而言,只知道 e、n 和密文,要破译 d 很难,因为最终需要推导 p 和 q 的值,而这涉及到对大整数的因式分解,目前还没有高效的算法可以解决这个问题。
ECC
ECC(Elliptic Curve Cryptography)算法是基于椭圆曲线的密码技术的统称,实际上包括非对称加密、数字签名和密钥交换三类。
ECC 使用椭圆曲线上的离散对数问题实现非对称加密,即已知椭圆曲线 E、E 上两点 G 和 xG,求解 x(参见椭圆曲线上的运算定义)。
通信双方只需要商定椭圆曲线上一点 G,确定各自的私钥 a、b,公钥则为 aG 和 bG,共享密钥则为 abG。
哈希函数
上面所提到的加密算法虽然可以保证数据的机密性,但是无法保证数据的完整性,攻击者就算无法破解密钥,也可以通过修改密文内容的方式来破坏数据,因此,我们最好能够对数据进行完整性校验,以便能及时发现数据被篡改的情况。
单向散列函数(One-way Hash Function)可以将任意长度的数据映射为固定长度的数据,这种映射是单向的,即无法通过散列值反推原始数据。在通信时,发送方将原始数据和散列值一起发送给接收方,接收方收到数据后,再次计算散列值,如果两个散列值不一致,则说明数据被篡改。
如同我们用哈希表存储数据时会遭遇哈希碰撞一样,这里的单向散列函数同样可能出现碰撞,即两条不同的消息可能产生相同的散列值,这就十分考验散列函数的设计了。
常见的单向散列函数有 MD5(MD 即 Message Digest)、SHA-1(SHA 即 Secure Hash Algorithm)、SHA-2、SHA-3 等,你在下载文件或者网络通信时应该或多或少见过。MD4、MD5 和 SHA-2 的抗碰撞性目前已经被攻破,现在主要使用 SHA-2 和 SHA-3(Keccak)
消息认证码
尽管哈希函数可以保证数据的完整性,但是无法保证数据的来源。攻击者大可以自己伪装成发送方,发送一条经过篡改的数据,并且附上正确的散列值,接收方只能判断这条消息没被第三方篡改,却无法辨别数据是否真的是由发送方发出的。
消息认证码(Message Authentication Code,MAC)既可以用于数据完整性校验,也可以用于数据来源认证。我们可以将其理解为带有密钥的哈希函数,这个密钥由通信双方持有。发送方发送数据时附带数据的 MAC 值,接收方可以利用自己的密钥计算数据的 MAC 值,如果两个值一致,则说明数据没有被篡改,且数据来源可信。
MAC 的密钥让我们联想到对称加密算法中的密钥配送问题,事实上,MAC 的密钥也需要通过非对称加密、DH 密钥协商等方式确保安全地传输。
数字签名
使用 MAC 可能出现这样的问题:A 收到 B 的消息,通过了 MAC 认证,但是 B 却否认发送过这条消息,并声称是 A 在本地伪造了这条消息。这个问题的根源是,通信双方同时持有 MAC 密钥,因此只能证明一条消息是其中某一方发出的(对于 A 来说,他只能认为收到的消息是 B 发出的),这就给了另一方抵赖的机会。
数字签名利用非对称加密的方式弥补了这个缺陷:
- 通信双方各自持有一个公钥 - 私钥对。
- 在通信过程中,双方拿到对方的公钥。
- 发送消息时,发送方用自己的私钥对消息进行签名。
- 接收消息时,接收方用对方的公钥对消息进行验证。
由于非对称加密解密算法较慢,我们一般只对消息的摘要(散列值)进行签名。
由于只有持有私钥的一方才能对消息进行签名,因此,即使前文中 B 否认发送过消息,A 也可以通过验证消息的签名来证明消息是 B 发出的。
注意,这样做仍然无法避免中间人攻击,这需要借助数字证书来解决,但这就不是密码学的范畴了。
伪随机数生成器
随机数广泛地用于生成密钥、密钥对、IV、nonce 和 salt 中,能帮助我们避免重放攻击、字典攻击等。
生成随机数需要满足三个性质:
- 随机性:不存在统计学偏差,即生成的随机数是均匀分布的。
- 不可预测性:无法通过已知的随机数推导出下一个随机数。
- 不可重现性:除非将随机数序列保存下来,否则无法重现之前生成过的序列。
硬件中生成随机数往往借助自然界中无法预测和重现的随机现象,如热噪声、温度和声音的变化等,而软件中无法追踪随机现象,故无法生成真随机数,只能是伪随机数。
一个伪随机数生成器需要借助外部的种子来初始化内部状态,然后根据内部状态生成随机数,同时更新内部状态。如果种子相同,那么生成的随机数序列也是相同的。